how to find vertical and horizontal asymptote

Related Pages
Reciprocal Functions
Hyperbolas
More than lessons on Calculus

The following diagram shows the different types of asymptotes: horizontal asymptotes, vertical asymptotes, and oblique asymptotes. Scroll downwardly the page for more examples and solutions on how to notice asymptotes.

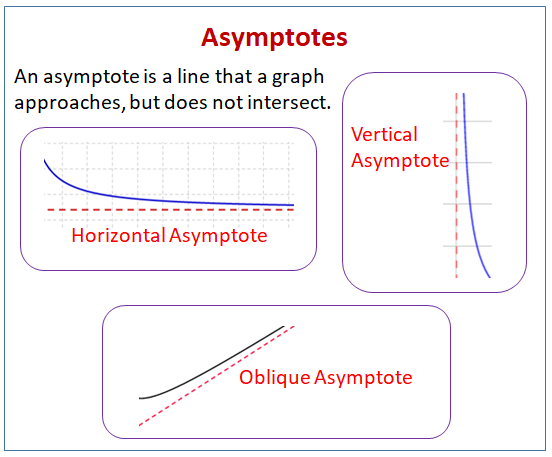
Vertical Asymptote

How to make up one's mind the Vertical Asymptote?

Method 1: Use the Definition of Vertical Asymptote

The line ten = a is called a Vertical Asymptote of the bend y = f(ten) if at least 1 of the following statements is true.

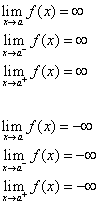
Method two:

For rational functions, vertical asymptotes are vertical lines that correspond to the zeroes of the denominator.

Given the rational function, f(10)

Step 1: Write f(x) in reduced form

Step 2: if x – c is a gene in the denominator and so x = c is the vertical asymptote.

Instance:
Notice the vertical asymptotes of

Solution:
Method 1: Utilize the definition of Vertical Asymptote.

If x is close to 3 but larger than 3, then the denominator x – 3 is a small positive number and 2x is shut to 8. So, is a large positive number.

Intuitively, we see that

Similarly, if x is shut to three but smaller than 3, then 10 – 3 is a minor negative number and 2x is close to 8. And then, is a large negative number.

The line x = three is the vertical asymptote.

Method 2:

Stride ane: f(x) is already in reduced form.

Step 2: The denominator is 10 – 3, and and so the Vertical Asymptote is at x = 3.

Finding Vertical Asymptotes of Rational Functions

What to look for, in order to discover vertical asymptotes of rational functions.

• Bear witness Video Lesson

Vertical Asymptotes of Rational Functions: Quick Style to Find Them

Example of finding vertical asymptotes of rational functions.

• Show Video Lesson

Horizontal Asymptote

How to make up one's mind the horizontal Asymptote?

Method i: Use the definition of Horizontal Asymptote

The line y = L is called a horizontal asymptote of the bend y = f(x) if either

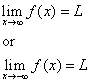
Method ii:

For the rational function, f(x)

If the caste of 10 in the numerator is less than the caste of x in the denominator then y = 0 is the horizontal asymptote.

If the degree of x in the numerator is equal to the degree of x in the denominator then y = c where c is obtained by dividing the leading coefficients.

Instance:
Observe the horizontal and vertical asymptotes of the office.

Solution:
Method one:

Divide both numerator and denominator by x.

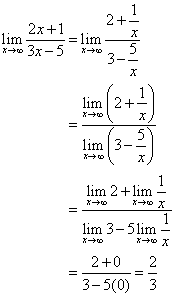
The line is the horizontal asymptote.

Method 2:

The degree of x in the numerator is equal to the degree of x in the denominator.

Dividing the leading coefficients we get

The line is the horizontal asymptote.

Shortcut to Find Horizontal Asymptotes of Rational Functions

A couple of tricks that make finding horizontal asymptotes of rational functions very easy to practice The degree of a function is the highest ability of x that appears in the polynomial. To observe the horizontal asymptote, there are three like shooting fish in a barrel cases.

1. If the degree of the numerator expression is less than the degree of the denominator expression, then the horizontal asymptote is y=0 (the x-axis).
   
2. If the degree of the numerator is equal to the degree of the denominator, then you can detect the horizontal asymptote by dividing the commencement, highest term of the numerator by the beginning, highest term of the denominator. This volition simplify to y = some abiding (just a number).
   
3. If the caste of the numerator is greater than the caste of the denominator, then there is no horizontal asymptote.

• Show Video Lesson

Oblique Asymptote or Slant Asymptote

Some curves accept asymptotes that are oblique, that is, neither horizontal nor vertical.

If then the line y = mx + b is called the oblique or slant asymptote because the vertical distances between the curve y = f(x) and the line y = mx + b approaches 0.

For rational functions, oblique asymptotes occur when the degree of the numerator is one more than the degree of the denominator. In such a case the equation of the oblique asymptote can be found by long division.

Instance:
Detect the asymptotes of the function

Solution:
Since the denominator x² + i is never 0, there is no vertical asymptote.

Since the degree of x in the numerator is greater than the degree of ten in the denominator in that location is no horizontal asymptote.

Since the degree of ten in the numerator is i greater than the degree of x in the denominator we can apply long division to obtain the oblique asymptote.

Then, the line y = ten is the oblique asymptote.

Finding Camber Asymptotes of Rational Functions

This video describes when a rational part has a slant asymptote, briefly depict what a slant asymptote is, and then practise 2 examples.

• Show Video Lesson

Find Asymptotes of a Rational Part (Vertical, Horizontal and Oblique/Slant)

This video shows how to find the vertical asymptotes and a slant / oblique asymptotes of a rational function.

• Testify Video Lesson

Finding All Asymptotes of a Rational Role (Vertical, Horizontal, Oblique / Slant)

Hither nosotros look at a function and find the vertical asymptote and also conclude that in that location are no horizontal asymptotes, but that an oblique asymptote does exist. We then use long division to discover the oblique asymptote.

• Show Video Lesson

Try the free Mathway reckoner and problem solver below to practice various math topics. Effort the given examples, or blazon in your own trouble and check your answer with the stride-by-stride explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Source: https://www.onlinemathlearning.com/asymptote.html

Posted by: davisexter1987.blogspot.com

Share this post