How To Find Locus Of A Point

Eugene is a qualified control/instrumentation engineer Bsc (Eng) and has worked as a programmer of electronics & software for SCADA systems.

© Eugene Brennan

The Parabola, a Mathematical Function

In this tutorial you'll learn about a mathematical role called the parabola. We'll cover the definition of the parabola get-go and how information technology relates to the solid shape called the cone. Next we'll explore dissimilar means in which the equation of a parabola can exist expressed. Likewise covered will be how to work out the maxima and minima of a parabola and how to observe the intersection with the x and y axes. Finally we'll discover what a quadratic equation is and how you can solve it.

Definition of a Parabola

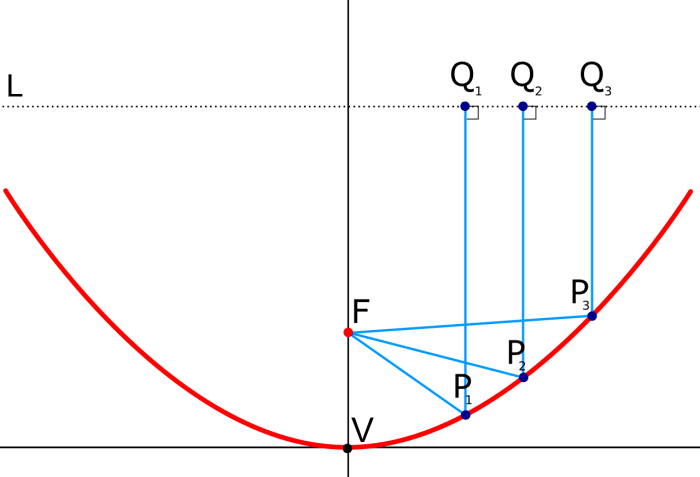
"A locus is a curve or other figure formed past all the points satisfying a detail equation."

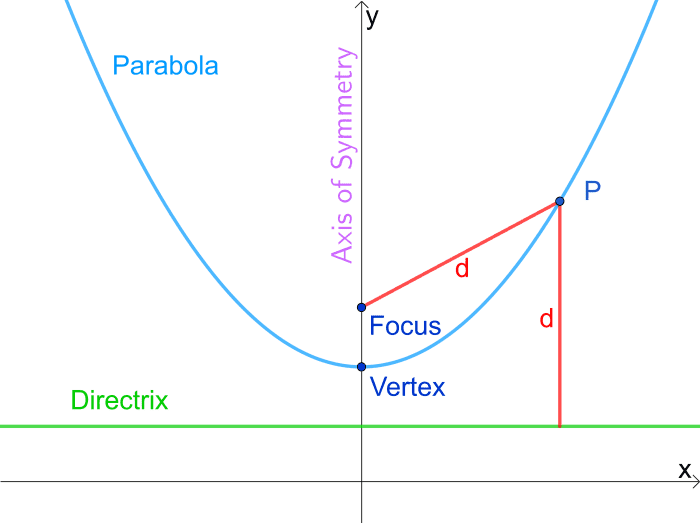
One way we tin ascertain a parabola is that it is the locus of points that are equidistant from both a line called the directrix and a point chosen the focus. So each point P on the parabola is the same distance from the focus as information technology is from the directrix every bit y'all can see in the animation beneath.

We notice also that when 10 is 0, the distance from P to the focus equals the altitude from the vertex to the directrix. And so the focus and directrix are equidistant from the vertex.

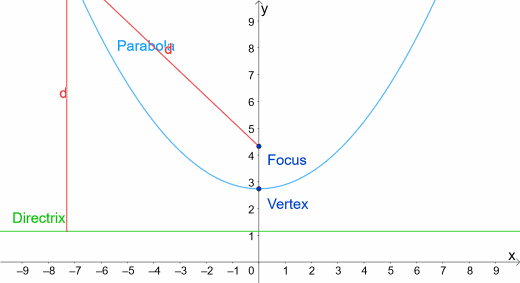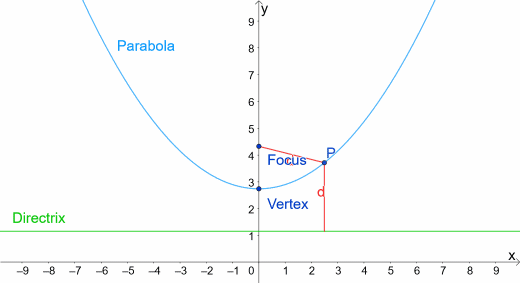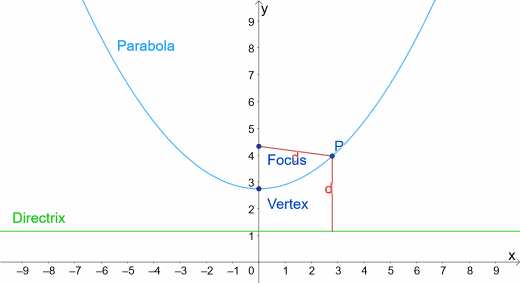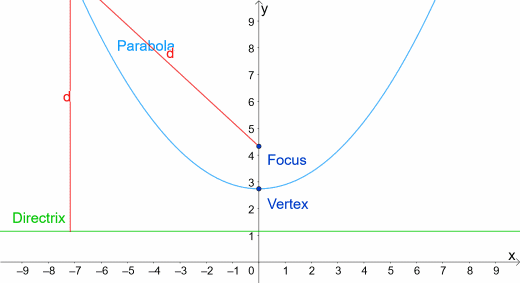
A parabola is a locus of points equidistant (the same distance) from a line called the directrix and point called the focus.

© Eugene Brennan

A Parabola is a Conic Section

Another mode of defining a parabola

When a plane intersects a cone, we become different shapes or conic sections where the aeroplane intersects the outer surface of the cone. If the plane is parallel to the bottom of the cone, nosotros just get a circumvolve. As the angle A in the animation below changes, information technology eventually becomes equal to B and the conic section is a parabola.

A parabola is the shape produced when a plane intersects a cone and the angle of intersection to the axis is equal to half the opening angle of the cone.

© Eugene Brennan

Equations of Parabolas

At that place are several ways we can limited the equation of a parabola:

• As a quadratic function
• Vertex form
• Focus course

We'll explore these later, but beginning let'southward await at the simplest parabola.

The Simplest Parabola y = x²

^{The simplest parabola with the vertex at the origin, point (0,0) on the graph, has the equation y = x².}

^{The value of y is merely the value of x multiplied past itself.}

Curl to Continue

Read More than From Owlcation

Graph of y = x²

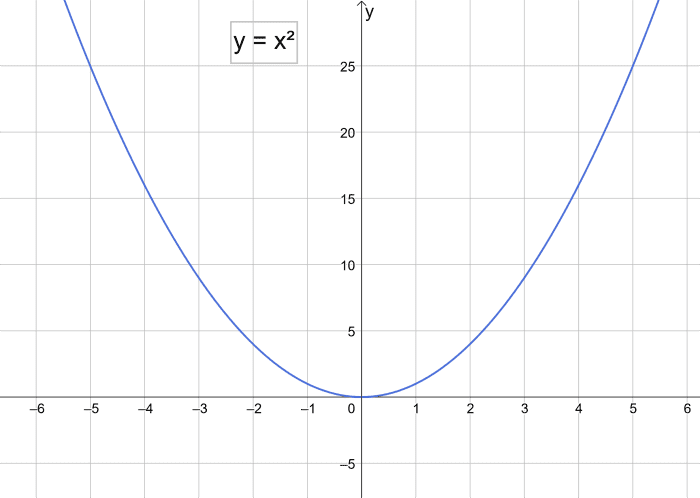
The simplest parabola, y = x²

© Eugene Brennan

Let's Give 10 a Coefficient!

The simplest parabola is y = 10^two but if we give x a coefficient, we tin generate an infinite number of parabolas with dissimilar "widths" depending on the value of the coefficient ɑ.

So lets brand y = ɑx²

In the graph beneath, ɑ has various values. Notice that when ɑ is negative, the parabola is "upside down". We'll discover more almost this later. Remember the y = ɑx² form of the equation of a parabola is when its vertex is at the origin.

Making ɑ smaller results in a "wider" parabola. If we make ɑ bigger, the parabola gets narrower.

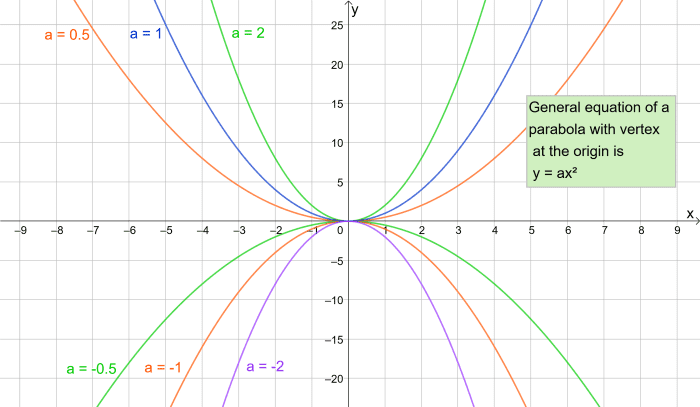
Parabolas with different coefficients of x²

© Eugene Brennan

Turning the Simplest Parabola on Its Side

If we plough the parabola y = x² on its side, we get a new function y² = x or x = y². This merely ways nosotros tin retrieve of y as being the independent variable and squaring it gives us the corresponding value for x.

So:

When y = two, 10 = y² = 4

when y = iii, x = y^two = 9

when y = 4, x = y² = xvi

and and then on...

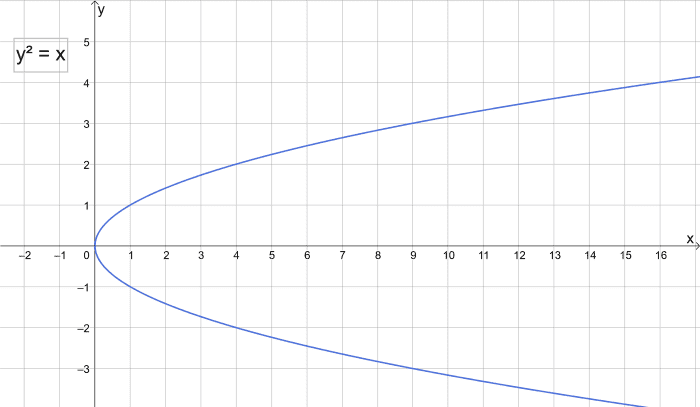
The parabola ten = y²

© Eugene Brennan

Just like the example of the vertical parabola, nosotros can once more add a coefficient to y^2.

So we take x = ɑy²

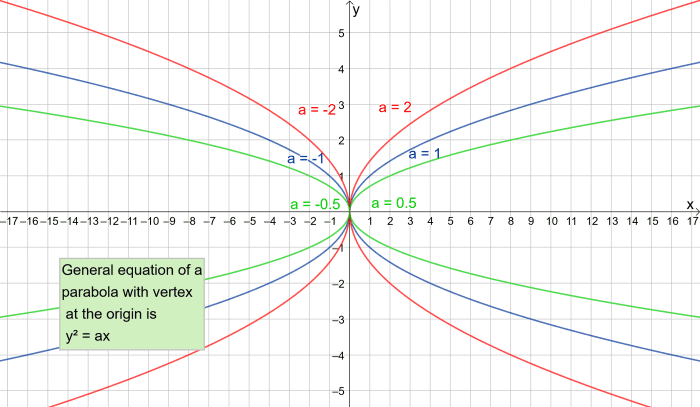
Parabolas with different coefficients of y²

© Eugene Brennan

Vertex Form of a Parabola Parallel to Y Centrality

One fashion we can express the equation of a parabola is in terms of the coordinates of the vertex. The equation depends on whether the axis of the parabola is parallel to the x or y axis, but in both cases, the vertex is located at the coordinates (h,1000). In the equations, ɑ is a coefficient and can have whatsoever value.

When the centrality is parallel to y axis:

y = ɑ(x - h)² + k

if ɑ = 1 and (h,k) is the origin (0,0) we go the simple parabola we saw at the commencement of the tutorial:

y = ane(x - 0)² + 0 = x²

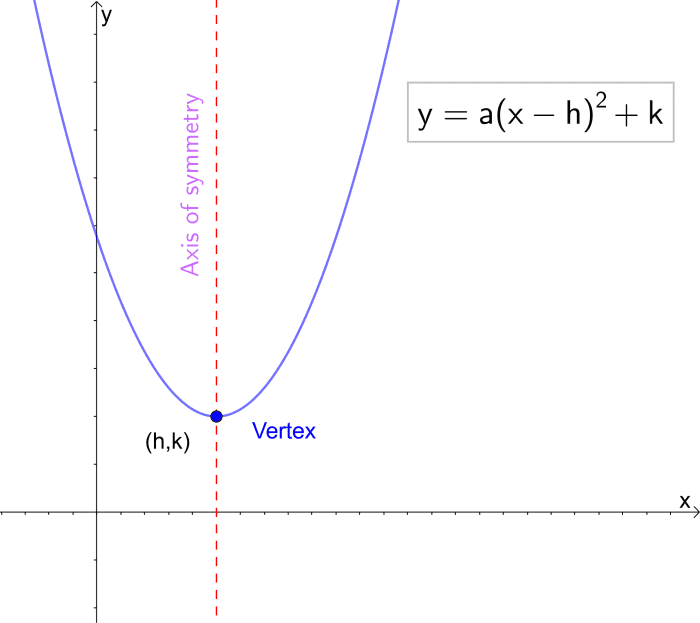
Vertex form of the equation of a parabola.

© Eugene Brennan

When the centrality is parallel to the x axis:

x = ɑ(y - h)² + k

Find that this doesn't requite u.s.a. any information about the location of the focus or directrix.

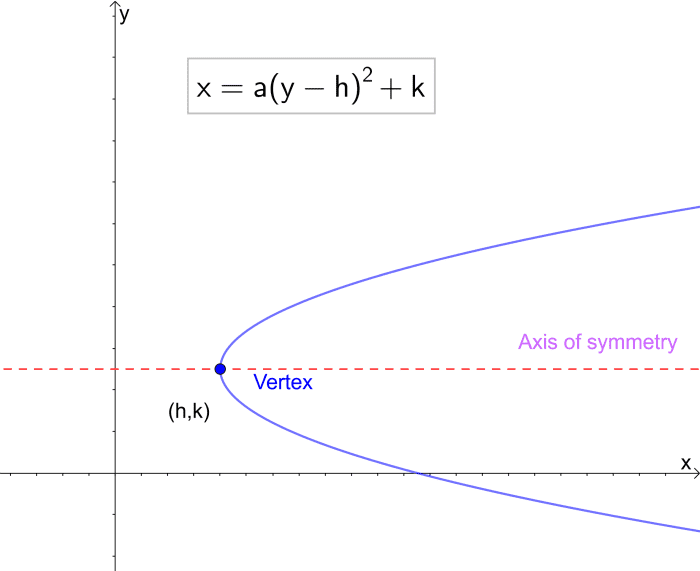
Vertex form of the equation of a parabola.

© Eugene Brennan

Equation of a Parabola in Terms of the Coordinates of the Focus

Another way of expressing the equation of a parabola is in terms of the coordinates of the vertex (h,thousand) and the focus.

Nosotros saw that:

y = ɑ(x - h)² + k

Using Pythagoras's Theorem we can testify that the coefficient ɑ = 1/4p, where p is the distance from the focus to the vertex.

When the axis of symmetry is parallel to y axis:

Substituting for ɑ = one/4p gives us:

y = ɑ(x - h)² + k = 1/(4p)(x - h)^two + k

Multiply both sides of the equation past 4p:

4py = (ten - h)^two + 4pk

Rearrange:

4p(y - thousand) = (ten - h)ⁱⁱ

or

(x - h)ⁱⁱ = 4p(y - yard)

Similarly:

When the axis of symmetry is parallel to x axis:

A similar derivation gives us:

(y - k)² = 4p(x - h)

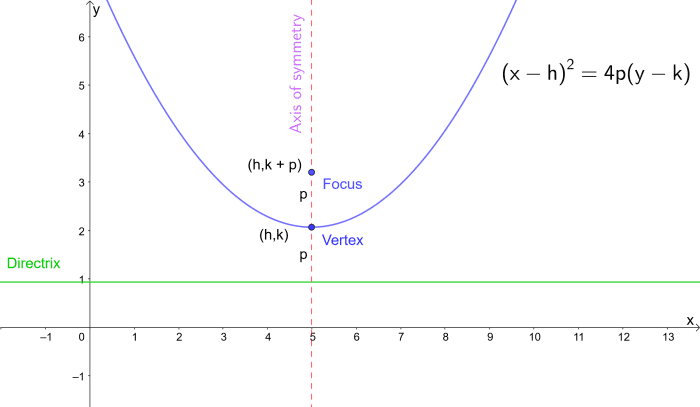
Equation of a parabola in terms of the focus. p is the distance from the vertex to the focus and vertex to the directrix.

© Eugene Brennan

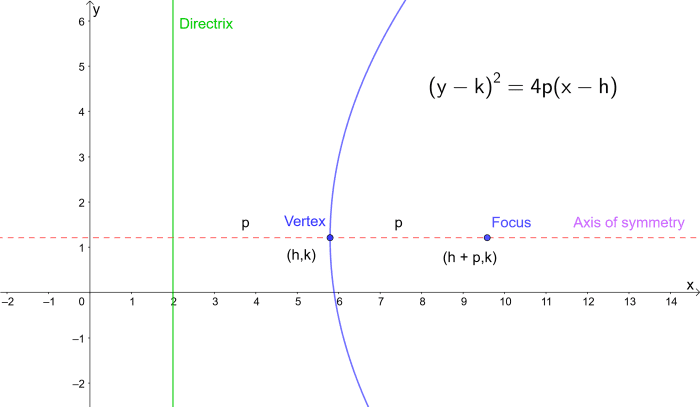
Focus form of the equation of a parabola. p is the altitude from the vertex to the focus and vertex to the directrix.

© Eugene Brennan

Example:

Find the focus for the simplest parabola y = xⁱⁱ

Reply:

Since the parabola is parallel to the y axis, we use the equation we learned well-nigh above

(x - h)² = 4p(y - 1000)

First detect the vertex, the point where the parabola intersects the y axis (for this uncomplicated parabola, we know the vertex occurs at x = 0)

So ready x = 0, giving y = ten² = 0^two = 0

and therefore the vertex occurs at (0,0)

But the vertex is (h,k), therefore h = 0 and k = 0

Substituting for the values of h and one thousand, the equation (x - h)ⁱⁱ = 4p(y - 1000) simplifies to

(x - 0)² = 4p(y - 0)

giving united states of america

10² = 4py

Now compare this to our original equation for the parabola y = x²

We can rewrite this every bit x^two = y, but the coefficient of y is 1, so 4p must equal 1 and p = i/iv.

From the graph above, we know the coordinates of the focus are (h, k + p), so substituting the values nosotros worked out for h, k and p gives us the coordinates of the vertex as

(0, 0 + ane/4) or (0, 1/4)

A Quadratic Function is a Parabola

Consider the function y = ɑx² + bx + c

This is called a quadratic role because of the square on the x variable.

This is some other style we can express the equation of a parabola.

How to Determine Which Direction a Parabola Opens

Irrespective of which form of equation that is used to depict a parabola, the coefficient of x^two determines whether a parabola will "open up" or "open down". Open up means that the parabola will accept a minimum and the value of y will increase on both sides of the minimum. Open downward ways it volition have a maximum and the value of y decreases on both sides of the max.

• If ɑ is positive, the parabola volition open upwardly
• If ɑ is negative the parabola will open down

Parabola Opens Upward or Opens Downwardly

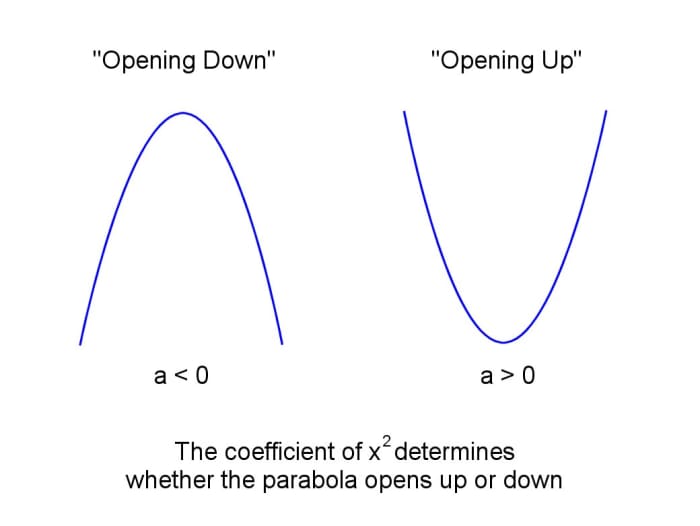
The sign of the coefficient of ten² determines whether a parabola opens upwardly or opens down.

© Eugene Brennan

How to Discover the Vertex of a Parabola

From uncomplicated calculus nosotros tin deduce that the max or min value of a parabola occurs at 10 = -b/2ɑ

Substitute for 10 into the equation y = ɑx² + bx + c to get the corresponding y value

And so y = ɑx² + bx + c

= ɑ(-b/2ɑ)² + b(-b/2ɑ) + c

= ɑ(b²/4ɑ^two) - b²/2ɑ + c

Collecting up the b^two terms and rearranging

= b² (ane/4ɑ - i/2ɑ) + c

= - b²/4ɑ + c

= c -b²/4a

So finally the min occurs at (-b/2ɑ, c -b²/4ɑ)

Example:

Find the vertex of the equation y = 5x² - 10x + 7

1. The coefficient a is positive, so the parabola opens up and the vertex is a minimum
2. ɑ = 5, b = -10 and c = 7, then the x value of the minimum occurs at 10 = -b/2ɑ = - (-10)/(two(5)) = 1
3. The y value of the min occurs at c - b^two/4a. Substituting for a, b and c gives us y = vii - (-x)² / (4(five)) = 7 - 100/xx = 7 - 5 = 2

So the vertex occurs at (i,2)

How to Discover the X-Intercepts of a Parabola

A quadratic function y = ɑx^two + bx + c is the equation of a parabola.

If nosotros set the quadratic part to zero, we become a quadratic equation

i.due east. ɑx^two + bx + c = 0 .

Graphically, equating the function to cipher means setting a status of the function such that the y value is 0, in other words, where the parabola intercepts the ten axis.

The solutions of the quadratic equation allow us to notice these ii points. If there are no real number solutions, i.e. the solutions are imaginary numbers, the parabola doesn't intersect the 10 axis.

The solutions or roots of a quadratic equation are given by the equation:

ten = -b ± √(b² -4ac) / 2ɑ

Finding the Roots of a Quadratic Equation

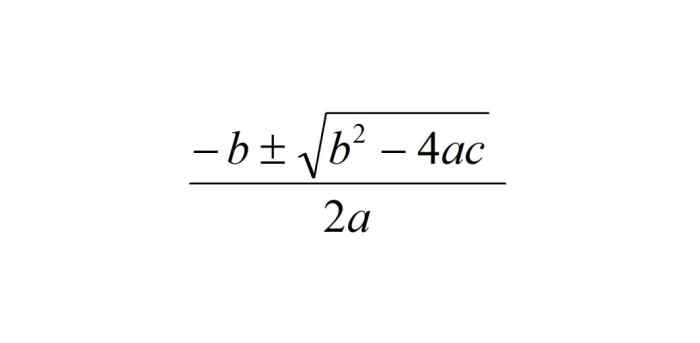
The roots of a quadratic equation give the x axis intercepts of a parabola.

© Eugene Brennan

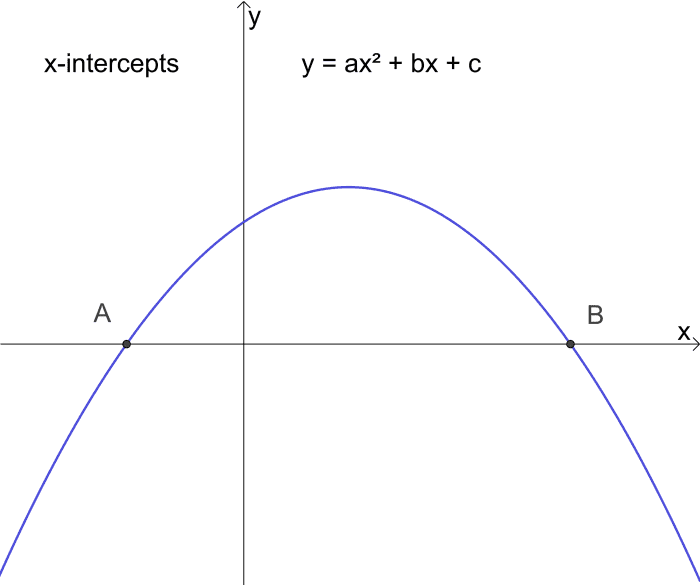
A and B are the x-intercepts of the parabola y = ax² + bx + c and roots of the quadratic equation ax² + bx + c = 0

© Eugene Brennan

Example one: Find the x-axis intercepts of the parabola y = 3x^two + 7x + ii

Solution

• y = ɑx² + bx + c

• In our example y = 3x² + 7x + ii

• Identify the coefficients and constant c

• And then ɑ = three, b = 7 and c = 2

• The roots of the quadratic equation 3x^two + 7x + 2 = 0 are at x = (-b ± √(b² - 4ɑc)) / 2ɑ

• Substitute for ɑ, b and c

• The starting time root is at x = (-7 + √(vii² - four ten 3 x 2)) / (2 x 3) = -1/3

• The second root is at (-7 - √(7^two - 4 x three x ii)) / (2 x 3) = -ii

• So the x centrality intercepts occur at (-ii, 0) and (-1/3, 0)

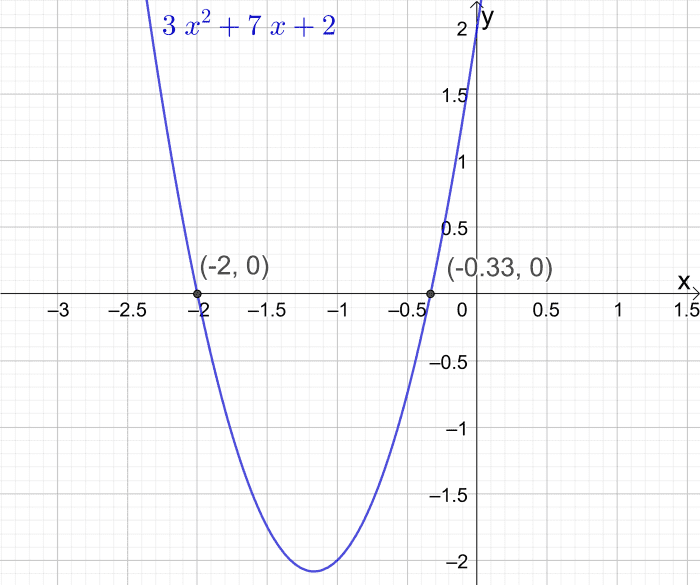
Example one: Find the x-intercepts of the parabola y = 3x2 + 7x + 2

© Eugene Brennan

Example 2: Find the x-axis intercepts of the parabola with vertex located at (4, 6) and focus at (4, 3)

Solution

• The equation of the parabola in focus vertex form is (x - h)ⁱⁱ = 4p(y - k)
• The vertex is at (h,k) giving united states h = iv, 1000 = 6
• The focus is located at (h, k + p). In this example the focus is at (4, 3) so k + p = iii. But k = vi then p = iii - half-dozen = -three
• Plug the values into the equation (10 - h)^two = 4p(y - k) then (x - 4)^two = 4(-3)(y - 6)
• Simplify giving (x - iv)² = -12(y - 6)
• Expand out the equation gives us 10^two - 8x + 16 = -12y + 72
• Rearrange 12y = -x^two + 8x + 56
• Giving y = -i/12x² + 2/3x + xiv/3

• The coefficients are a = -1/12, b = 2/3, c = xiv/3

• The roots are at (-2/3 ± √((two/3)ⁱⁱ - four(-1/12)(14/3)))/(2(-1/12)

• This gives usa x = -4.49 approx and x = 12.49 approx
• So the x axis intercepts occur at (-4.49, 0) and (12.49, 0)

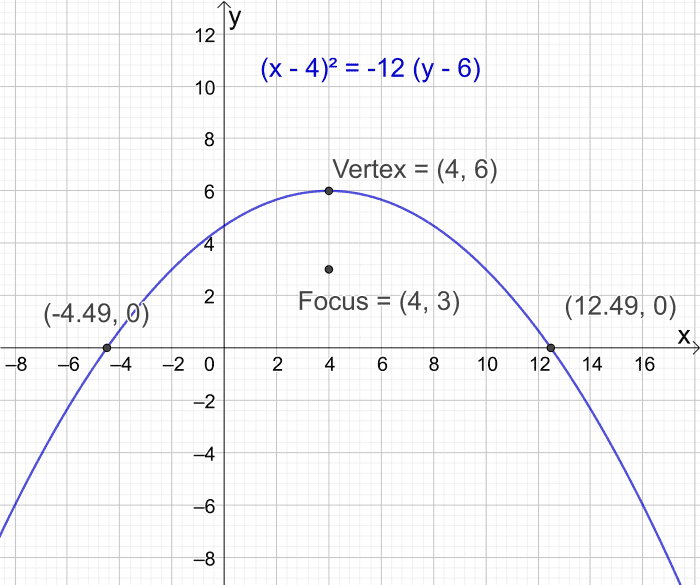
Example two: Detect the x-intercepts of the parabola with vertex at (4, 6) and focus at (iv, 3)

© Eugene Brennan

How to Find the Y-Intercepts of a Parabola

To detect the y-axis intercept (y-intercept) of a parabola, we set up x to 0 and summate the value of y.

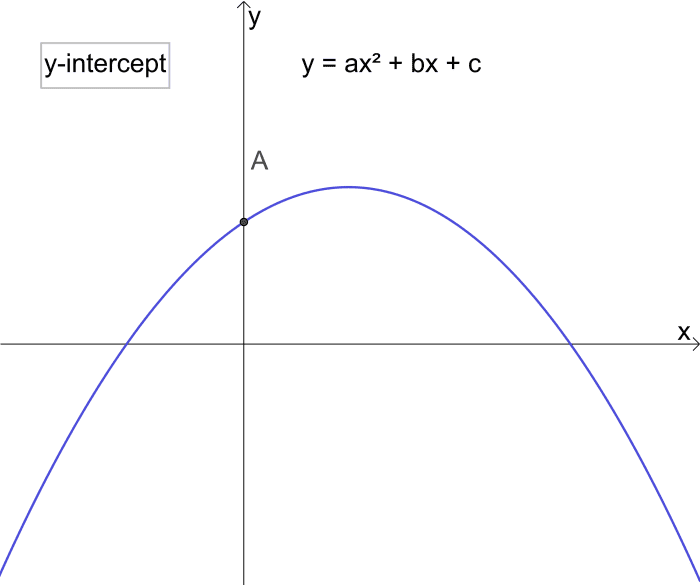
A is the y-intercept of the parabola y = ax² + bx + c

© Eugene Brennan

Example 3: Detect the y-intercept of the parabola y = 6x² + 4x + 7

Solution:

y = 6x² + 4x + 7

Set x to 0 giving

y = 6(0)² + iv(0) + 7 = vii

The intercept occurs at (0, vii)

Case three: Find the y-intercept of the parabola y = 6x² + 4x + 7

© Eugene Brennan

Summary of Parabola Equations

For a parabola with axis parallel to the y-centrality, (h,k) is the vertex and (h, grand+ p) is the focus.

Equation Blazon	Axis Parallel to Y-Axis	Centrality Parallel to 10-Axis
Quadratic Office	y = ɑx² + bx + c	x = ɑy² + by + c
Vertex Class	y = ɑ(x - h)² + k	x = ɑ(y - h)² + k
Focus Form	(ten - h)² = 4p(y - one thousand)	(y - k)² = 4p(x - h)
Parabola with Vertex at the Origin	ten² = 4py	y² = 4px
Roots of a parabola parallel to y axis	x = -b ± √( b² -4ɑc)/2ɑ
Vertex occurs at	(-b/2ɑ, c -b2/4ɑ)

How the Parabola is Used in the Real World

The parabola isn't just confined to math. The parabola shape appears in nature and we apply it in science and engineering science because of its properties.

• When you kick a ball into the air or a projectile is fired, the trajectory is a parabola
• The reflectors of vehicle headlights or flashlights are parabolic shaped
• The mirror in a reflecting telescope is parabolic
• Satellite dishes are in the shape of a parabola equally are radar dishes
• Microphones for listening to fain sounds tin can have parabolic reflectors fitted to collect audio. The microphone is located at the focus to collect sound.

For radar dishes, satellite dishes and radio and optical telescopes, one of the parabola's properties is that a ray of electromagnetic radiations parallel to its axis will be reflected towards the focus. Conversely in the case of a headlight or torch, light coming from the focus will be reflected off the reflector and travel outwards in a parallel beam.

Related reading: Deriving Projectile Movement Equations

Radar dishes and radio telescopes are parabolic shaped.

Wikiimages, public domain epitome via Pixabay.com

Parabolic Reflector

Images parallel to the axis are reflected through the focus of a parabola. Similarly light rays leaving the focus are reflected off the parabola and travel parallel to the axis.

Public domain prototype via Wikimedia Commons

Water from a fountain (which can be considered as a stream of particles) follows a parabolic trajectory

GuidoB, CC past SA 3.0 Unported via Wikimedia Eatables

Acknowledgements

All graphics were created using GeoGebra Classic.

© 2019 Eugene Brennan

Srinjan Sanyal on May 27, 2020:

the content is very good.

rafia from lahore pakistna on September 29, 2019:

hey y'all are a dainty teacher! i previously did not know the open up up or down graph ..but now i do ..thank yous!

Source: https://owlcation.com/stem/How-to-Understand-the-Equation-of-a-Parabola-Directrix-and-Focus

Posted by: davisexter1987.blogspot.com

Share this post